|
|
 |
The PageRank Algorithm
|
 |
|
 |
The original PageRank algorithm was
described by Lawrence Page and Sergey Brin in several
publications. It is given by
PR(A) = (1-d) + d
(PR(T1)/C(T1) + ... + PR(Tn)/C(Tn))
where
- PR(A) is the PageRank of page A,
- PR(Ti) is the PageRank of pages Ti which link to
page A,
- C(Ti) is the number of outbound links on page Ti and
- d is a damping factor which can be set between
0 and 1.
So, first of all, we see that
PageRank does not rank web sites as a whole, but is determined
for each page individually. Further, the PageRank of page A is
recursively defined by the PageRanks of those pages which link
to page A.
The PageRank of pages Ti which link to page
A does not influence the PageRank of page A uniformly. Within
the PageRank algorithm, the PageRank of a page T is always
weighted by the number of outbound links C(T) on page T. This
means that the more outbound links a page T has, the less will
page A benefit from a link to it on page T.
The
weighted PageRank of pages Ti is then added up. The outcome of
this is that an additional inbound link for page A will always
increase page A's PageRank.
Finally, the sum of the
weighted PageRanks of all pages Ti is multiplied with a
damping factor d which can be set between 0 and 1. Thereby,
the extend of PageRank benefit for a page by another page
linking to it is reduced. |
|
|
The Random Surfer Model
|
|
|
|
In their publications, Lawrence Page and Sergey Brin
give a very simple intuitive justification for the PageRank
algorithm. They consider PageRank as a model of user
behaviour, where a surfer clicks on links at random with no
regard towards content.
The random surfer visits a web
page with a certain probability which derives from the page's
PageRank. The probability that the random surfer clicks on one
link is solely given by the number of links on that page. This
is why one page's PageRank is not completely passed on to a
page it links to, but is devided by the number of links on the
page.
So, the probability for the random surfer
reaching one page is the sum of probabilities for the random
surfer following links to this page. Now, this probability is
reduced by the damping factor d. The justification within the
Random Surfer Model, therefore, is that the surfer does not
click on an infinite number of links, but gets bored sometimes
and jumps to another page at random.
The probability
for the random surfer not stopping to click on links is given
by the damping factor d, which is, depending on the degree of
probability therefore, set between 0 and 1. The higher d is,
the more likely will the random surfer keep clicking links.
Since the surfer jumps to another page at random after he
stopped clicking links, the probability therefore is
implemented as a constant (1-d) into the algorithm. Regardless
of inbound links, the probability for the random surfer
jumping to a page is always (1-d), so a page has always a
minimum PageRank. |
|
|
A Different Notation of the PageRank
Algorithm
|
|
|
|
Lawrence Page and Sergey Brin have published two
different versions of their PageRank algorithm in different
papers. In the second version of the algorithm, the PageRank
of page A is given as
PR(A) = (1-d) / N + d
(PR(T1)/C(T1) + ... + PR(Tn)/C(Tn))
where N is the
total number of all pages on the web. The second version of
the algorithm, indeed, does not differ fundamentally from the
first one. Regarding the Random Surfer Model, the second
version's PageRank of a page is the actual probability for a
surfer reaching that page after clicking on many links. The
PageRanks then form a probability distribution over web pages,
so the sum of all pages' PageRanks will be one.
Contrary, in the first version of the algorithm the
probability for the random surfer reaching a page is weighted
by the total number of web pages. So, in this version PageRank
is an expected value for the random surfer visiting a page,
when he restarts this procedure as often as the web has pages.
If the web had 100 pages and a page had a PageRank value of 2,
the random surfer would reach that page in an average twice if
he restarts 100 times.
As mentioned above, the two
versions of the algorithm do not differ fundamentally from
each other. A PageRank which has been calculated by using the
second version of the algorithm has to be multiplied by the
total number of web pages to get the according PageRank that
would have been caculated by using the first version. Even
Page and Brin mixed up the two algorithm versions in their
most popular paper "The Anatomy of a Large-Scale Hypertextual
Web Search Engine", where they claim the first version of the
algorithm to form a probability distribution over web pages
with the sum of all pages' PageRanks being one.
In the
following, we will use the first version of the algorithm. The
reason is that PageRank calculations by means of this
algorithm are easier to compute, because we can disregard the
total number of web pages. |
|
|
The Characteristics of PageRank
|
|
|
|
The characteristics of PageRank shall be illustrated by
a small example.
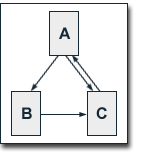 We
regard a small web consisting of three pages A, B and C,
whereby page A links to the pages B and C, page B links to
page C and page C links to page A. According to Page and Brin,
the damping factor d is usually set to 0.85, but to keep the
calculation simple we set it to 0.5. The exact value of the
damping factor d admittedly has effects on PageRank, but it
does not influence the fundamental principles of PageRank. So,
we get the following equations for the PageRank calculation: We
regard a small web consisting of three pages A, B and C,
whereby page A links to the pages B and C, page B links to
page C and page C links to page A. According to Page and Brin,
the damping factor d is usually set to 0.85, but to keep the
calculation simple we set it to 0.5. The exact value of the
damping factor d admittedly has effects on PageRank, but it
does not influence the fundamental principles of PageRank. So,
we get the following equations for the PageRank calculation:
PR(A) = 0.5 + 0.5 PR(C)
PR(B) = 0.5 + 0.5 (PR(A) /
2)
PR(C) = 0.5 + 0.5 (PR(A) / 2 + PR(B))
These
equations can easily be solved. We get the following PageRank
values for the single pages:
PR(A) = 14/13 =
1.07692308
PR(B) = 10/13 = 0.76923077
PR(C) = 15/13 =
1.15384615
It is obvious that the sum of all pages'
PageRanks is 3 and thus equals the total number of web pages.
As shown above this is not a specific result for our simple
example.
For our simple three-page example it is easy
to solve the according equation system to determine PageRank
values. In practice, the web consists of billions of documents
and it is not possible to find a solution by inspection.
|
|
|
The Iterative Computation of PageRank |
|
|
|
Because of the size of the actual web, the Google
search engine uses an approximative, iterative computation of
PageRank values. This means that each page is assigned an
initial starting value and the PageRanks of all pages are then
calculated in several computation circles based on the
equations determined by the PageRank algorithm. The iterative
calculation shall again be illustrated by our three-page
example, whereby each page is assigned a starting PageRank
value of 1.
| Iteration |
PR(A) |
PR(B) |
PR(C) |
| 0 |
1 |
1 |
1 |
| 1 |
1 |
0.75 |
1.125 |
| 2 |
1.0625 |
0.765625 |
1.1484375 |
| 3 |
1.07421875 |
0.76855469 |
1.15283203 |
| 4 |
1.07641602 |
0.76910400 |
1.15365601 |
| 5 |
1.07682800 |
0.76920700 |
1.15381050 |
| 6 |
1.07690525 |
0.76922631 |
1.15383947 |
| 7 |
1.07691973 |
0.76922993 |
1.15384490 |
| 8 |
1.07692245 |
0.76923061 |
1.15384592 |
| 9 |
1.07692296 |
0.76923074 |
1.15384611 |
| 10 |
1.07692305 |
0.76923076 |
1.15384615 |
| 11 |
1.07692307 |
0.76923077 |
1.15384615 |
| 12 |
1.07692308 |
0.76923077 |
1.15384615 |
We
see that we get a good approximation of the real PageRank
values after only a few iterations. According to publications
of Lawrence Page and Sergey Brin, about 100 iterations are
necessary to get a good approximation of the PageRank values
of the whole web.
Also, by means of the iterative
calculation, the sum of all pages' PageRanks still converges
to the total number of web pages. So the average PageRank of a
web page is 1. The minimum PageRank of a page is given by
(1-d). Therefore, there is a maximum PageRank for a page which
is given by dN+(1-d), where N is total number of web pages.
This maximum can theoretically occur, if all web pages solely
link to one page, and this page also solely links to itself.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PageRank and Google are trademarks of Google Inc.,
Mountain View CA, USA.
PageRank is protected by US Patent
6,285,999.
The content of this document may be
reproduced on the web provided that a copyright notice is
included and that there is a straight HTML hyperlink to the
corresponding page at pr.efactory.de in direct
context. |
|
|
|
| |
|